Generalização da mecânica estatística possibilita regularizar a teoria dos fenômenos críticos

Estudo coordenado pelo pesquisador da Unesp Mariano de Souza teve a participação de Constantino Tsallis, criador da mecânica estatística não extensiva. Resultados foram divulgados na revista Physical Review B

José Tadeu Arantes | Agência FAPESP – A mecânica estatística é um dos pilares da física moderna, e Ludwig Boltzmann (1844-1906) e Josiah Willard Gibbs (1839-1903) foram seus principais formuladores. Ambos trabalharam para estabelecer uma ponte entre a física macroscópica (descrita pela termodinâmica) e a física microscópica (baseada no comportamento de átomos e moléculas). O físico austríaco Boltzmann explicou a segunda lei da termodinâmica em termos estatísticos. E definiu a entropia de um sistema com base no número de microestados possíveis que tal sistema possa assumir. Diferentemente de Boltzmann, que se concentrou mais na física dos gases e na distribuição de partículas em equilíbrio, o norte-americano Gibbs desenvolveu um formalismo matemático geral, extensível a sistemas mais complexos. Juntas, as contribuições dos dois formaram a base de uma física capaz de modelar uma grande variedade de fenômenos.

Porém, a mecânica estatística de Boltzmann-Gibbs tem limitações, pois quando um sistema se encontra em determinados regimes, como transições de fase ou fenômenos críticos, suas predições podem falhar. Por exemplo, a mecânica estatística prediz a divergência de certas grandezas termodinâmicas em pontos críticos, algo que não é observado experimentalmente. Isso motivou o desenvolvimento da chamada “mecânica estatística não extensiva”, proposta pelo físico greco-brasileiro Constantino Tsallis, que constitui uma generalização da mecânica estatística de Boltzmann-Gibbs-von Neumann-Shannon.

Um novo estudo, liderado por Mariano de Souza na Universidade Estadual Paulista (Unesp), em colaboração com Constantino Tsallis, no Centro Brasileiro de Pesquisas Físicas (CBPF), enfocou o problema da divergência em pontos críticos. Os resultados foram publicados na revista Physical Review B em formato Letter.

“A entropia quantifica o número de microestados possíveis de um sistema. No contexto da mecânica estatística de Boltzmann-Gibbs, essa entropia é extensiva, ou seja, cresce proporcionalmente ao tamanho do sistema. No entanto, em pontos críticos e transições de fase, essa extensividade pode ser violada devido ao surgimento de correlações de longo alcance entre as partículas. Isso faz com que a abordagem tradicional preveja a divergência de quantidades como suscetibilidade magnética isotérmica e o coeficiente de expansão térmica, algo que não condiz com a realidade experimental”, diz Souza.

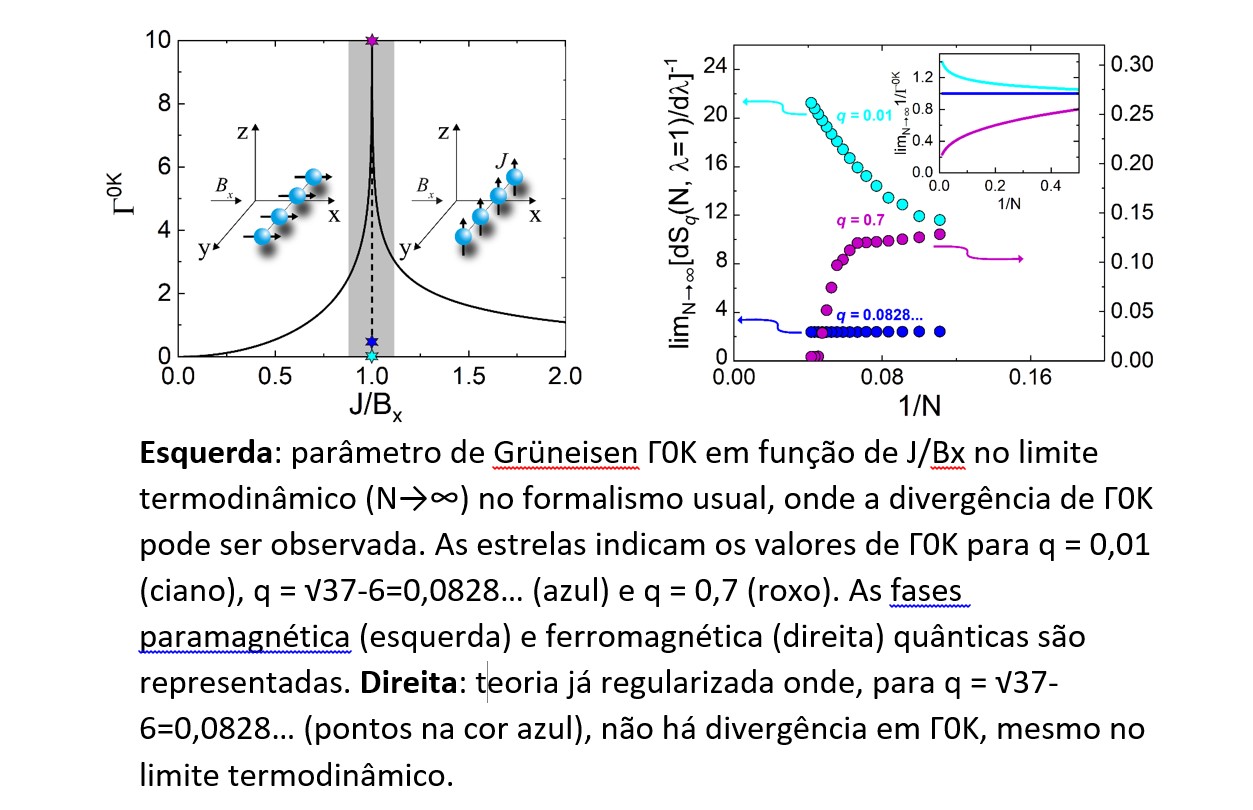
E continua: “Uma ferramenta amplamente utilizada para estudar esses fenômenos é o parâmetro de Grüneisen (Γ), que relaciona a expansão térmica ao calor específico do material. Segundo a mecânica estatística de Boltzmann-Gibbs, esse parâmetro também deveria divergir em pontos críticos. Contudo, na prática, não é possível medir valores infinitos para grandezas físicas, indicando que a teoria precisa ser regularizada”.

Em 1988, baseado no conceito de multifractais, Tsallis propôs uma generalização da entropia de Boltzmann-Gibbs-von Neumann-Shannon, conhecida como entropia não aditiva S_q. Essa formulação introduz um índice entrópico (q), que permite ajustar a maneira como as probabilidades são contabilizadas no cálculo da entropia. Em situações usuais, a teoria de Boltzmann-Gibbs é preservada. No entanto, em sistemas que apresentam fenômenos críticos, um valor específico de q pode restaurar a extensividade da entropia e eliminar as divergências previstas pela teoria tradicional.

“Inspirados por essa abordagem, reformulamos o parâmetro de Grüneisen em termos S_q. Para isso, utilizamos a versão quântica do parâmetro de Grüneisen, Γ^0K, para estudar um dos modelos mais simples que apresentam um ponto crítico quântico: o modelo de Ising unidimensional sob a ação de um campo magnético transverso, conforme a figura 1. Os resultados mostraram que o limite de Γ^0K é infinito para q > q_especial, zero para q < q_especial e finito e não nulo somente para q = q_especial, sendo q_especial o valor do índice q que recupera a extensividade da entropia. Ou seja, enquanto a teoria convencional previa uma divergência em pontos críticos, a nova abordagem baseada na entropia não aditiva regulariza essas divergências e fornece valores finitos e consistentes com as observações experimentais”, relata Souza.

Os resultados do estudo abrem novas perspectivas para a compreensão de fenômenos críticos em sistemas complexos. A regularização da teoria pode ser aplicada a uma variedade de sistemas, desde materiais magnéticos até sistemas de matéria condensada e dinâmica de fluidos quânticos. “Acreditamos que essa abordagem pode fornecer insights valiosos sobre fenômenos críticos em diferentes contextos”, comenta Souza.

Além de Souza e Tsallis, o estudo teve a participação do mestrando Samuel Martignago Soares e do pós-doutorando Lucas Squillante, ambos da equipe de Souza, e do pós-doutorando Henrique Santos Lima, do CBPF. O trabalho recebeu apoio financeiro da FAPESP por meio do projeto “Investigação das propriedades termodinâmicas e de transporte de sistemas eletrônicos fortemente correlacionados”.

O artigo Universally Nondiverging Grüneisen Parameter at Critical Points pode ser acessado em: https://journals.aps.org/prb/abstract/10.1103/PhysRevB.111.L060409.